Оглавление:
- Шаг 1. Знакомство с таблицами истинности
- Шаг 2: знание символов
- Шаг 3: форматирование таблицы
- Шаг 4: присвоение истинности и ложности
- Шаг 5: отрицание
- Шаг 6: переменная "q"
- Шаг 7: поиск неверных значений в последнем столбце
- Шаг 8: поиск истины в последнем столбце
- Шаг 9: Завершение стола
- Шаг 10: Готово
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 11:49.
- Последнее изменение 2025-01-23 15:04.

Таблица истинности - это способ визуализировать все результаты проблемы. Этот набор инструкций предназначен для людей, начинающих заниматься дискретной математикой. Сегодня мы будем практиковаться с примером задачи, относящейся к этим инструкциям. Вам понадобится бумага для заметок и карандаш, чтобы визуализировать стол. Эта задача должна занять около 5 минут для людей, уже знакомых с темой, и около 10 минут для новичков.
Для этого набора команд мы сосредоточимся на проблеме ~ p Λ q. Мы используем это, чтобы ввести некоторые символы, необходимые для интерпретации таблиц истинности.
Шаг 1. Знакомство с таблицами истинности

Таблица истинности - это способ визуализировать все возможности проблемы. Знание таблиц истинности является основной необходимостью для дискретной математики. Здесь мы найдем все результаты для простого уравнения ~ p Λ q.
Шаг 2: знание символов

Первый шаг к таблице истинности - понимание знаков. Знак «~» в этой конкретной задаче означает отрицание. «P» и «q» являются переменными. «Λ» эквивалентно «и». Это уравнение читается как «не p и q», что означает, что уравнение истинно, если p неверно, а q истинно.
Шаг 3: форматирование таблицы

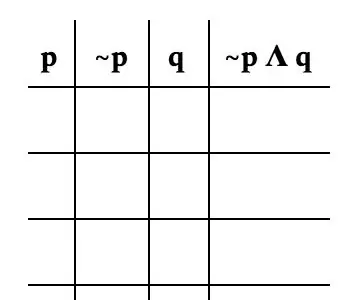
Теперь составим собственно таблицу. Важно разбить проблему по каждой переменной. Для этой задачи мы будем разбивать ее следующим образом: p, ~ p, q и ~ p Λ q. Изображение - хороший пример того, как должен выглядеть ваш стол.
Шаг 4: присвоение истинности и ложности

Поскольку есть только две переменные, для каждой переменной будет только четыре возможности. Для p мы разделяем его на половину пространств, занятых T (для истины), а другую половину - на F (для false).
Шаг 5: отрицание

Вместо ~ p вы пишете знак, противоположный значению p, поскольку ~ p является противоположностью p.
Шаг 6: переменная "q"

Для q вы чередуете T и F, чтобы получить каждую возможную комбинацию. Поскольку уравнение фокусируется только на ~ p, мы можем игнорировать столбец p при определении истинности уравнения. Символ «Λ» означает, что и ~ p, и q должны быть истинными, чтобы уравнение было истинным.
Шаг 7: поиск неверных значений в последнем столбце

Для первой строки, поскольку ~ p - это F, а q - это T, ~ p Λ q - это F в сценарии, в котором ~ p - это F, а q - T. Единственный сценарий, в котором уравнение T - это где ~ p - T, а q - Т.
Шаг 8: поиск истины в последнем столбце

Это означает, что единственная строка, которая является T, является третьей.
Шаг 9: Завершение стола

Дважды проверьте правильность вашей таблицы. Вы делаете это, проверяя правильность своих знаков и убедившись, что последний столбец написан правильно. Последний столбец - это результат всех возможных перестановок переменных.
Шаг 10: Готово
Теперь, когда вы знаете, как составить базовую таблицу истинности, продолжайте практиковаться! Чем больше вы практикуетесь, тем лучше вы будете их выполнять.
Рекомендуемые:
Решение для светового загрязнения - Artemis: 14 шагов

Решение проблемы светового загрязнения - Артемида: Световое загрязнение - это то, что затрагивает всех нас во всем мире. С тех пор, как была изобретена лампочка, свет стал гораздо более популярен и особенно широко использовался в больших городах, таких как Нью-Йорк и Чикаго. Весь этот свет может повлиять на
Данные о погоде с использованием Google Таблиц и Google Script: 7 шагов

Данные о погоде с использованием Google Sheets и Google Script: в этом Blogtut мы собираемся отправлять показания датчика SHT25 в таблицы Google с помощью Adafruit huzzah ESP8266, который помогает отправлять данные в Интернет. Отправка данных в ячейку таблицы Google очень полезна. и простой способ, который сохраняет данные в
Потоковая передача данных из Google Таблиц на панель инструментов: 6 шагов
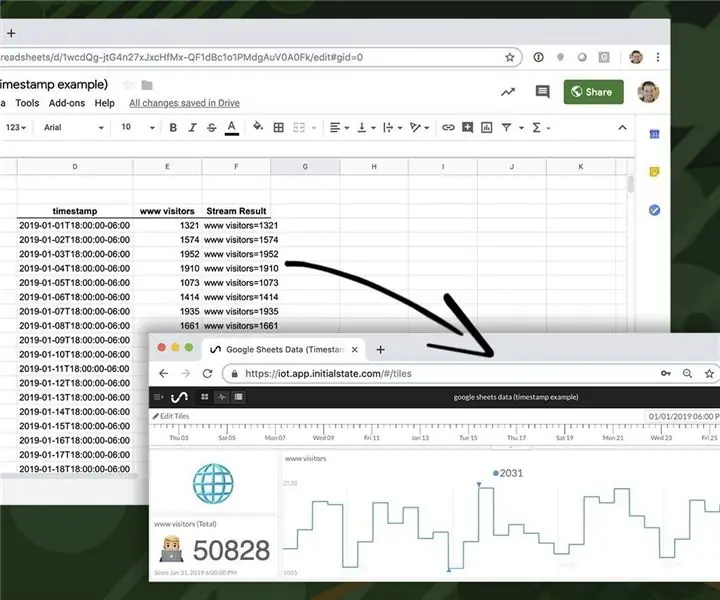
Потоковая передача данных из таблиц Google на панель инструментов. Таблицы превосходно обрабатывают данные, но не отображают их. Именно поэтому появилось так много компаний, занимающихся специализированной визуализацией данных и панелями бизнес-аналитики. Проблема с большинством этих продуктов заключается в том, что они обычно дороги и
Решение IOT для совместного использования велосипеда: 6 шагов
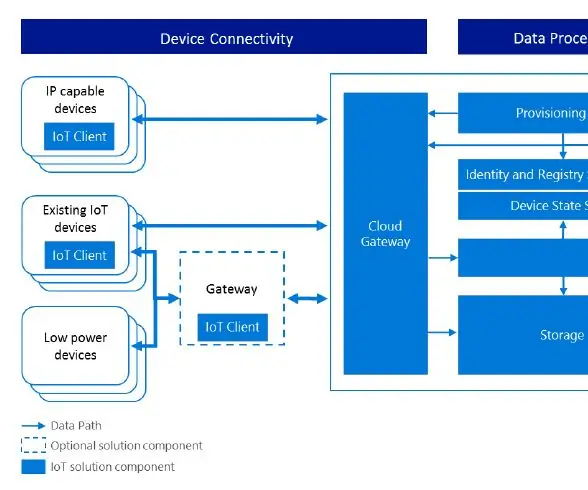
Решение IOT для совместного использования велосипеда. В наши дни в Китае очень популярен общий велосипед. На рынке представлено более 10 марок велосипедов для шеринга, и «мобайк» является самым известным, у него более 100 миллионов зарегистрированных пользователей, и он распространился на другие города, чем
Полное решение Arduino Rotary: 5 шагов

Полное решение для поворотных устройств Arduino: поворотные энкодеры - это поворотные ручки управления для электронных проектов, часто используемые с микроконтроллерами семейства Arduino. Их можно использовать для точной настройки параметров, навигации по меню, перемещения объектов на экране, установки значений любого типа. Они обычные заменители
