
Оглавление:
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 11:53.
- Последнее изменение 2025-01-23 15:05.



В этом руководстве я покажу вам, как создать игру в крестики-нолики с ИИ, используя Arduino. Вы можете играть против Arduino или смотреть, как Arduino играет против самого себя.
Я использую алгоритм под названием «алгоритм минимакса», который можно использовать не только для создания ИИ для Tic Tac Toe, но и для множества других игр, таких как «Четыре в ряд», шашки или даже шахматы. Такие игры, как шахматы, очень сложны и требуют гораздо более совершенных версий алгоритма. Для нашей игры Tic Tac Toe мы можем использовать простейшую версию алгоритма, которая, тем не менее, довольно впечатляет. На самом деле ИИ настолько хорош, что превзойти Ардуино невозможно!
Игра проста в сборке. Вам понадобится всего несколько компонентов и набросок, который я написал. Я также добавил более подробное объяснение алгоритма, если вы хотите понять, как он работает.
Шаг 1. Собери и играй
Для создания игры Tic Tac Toe вам потребуются следующие компоненты:
- Arduino Uno
- 9 светодиодов WS2812 RGB
- 9 кнопок
- некоторые провода и соединительные кабели
Подключите компоненты, как показано на эскизе Fritzing. Затем загрузите код в свой Arduino.
По умолчанию Arduino делает первый ход. Чтобы было немного интереснее, первый ход выбирается случайным образом. После первого хода Arduino использует алгоритм минимакса для определения наилучшего возможного хода. Вы начинаете новую игру, перезагружая Arduino.
Вы можете наблюдать, как Arduino «думает», открыв Serial Monitor. Для каждого возможного хода алгоритм вычисляет рейтинг, который указывает, приведет ли этот ход к выигрышу (значение 10) или проигрышу (значение -10) для Arduino или ничьей (значение 0).
Вы также можете посмотреть, как Arduino играет против самого себя, раскомментировав строку "#define DEMO_MODE" в самом начале скетча. Если вы загрузите измененный эскиз, Arduino сделает первый ход случайным образом, а затем использует алгоритм минимакса, чтобы определить лучший ход для каждого игрока на каждом ходу.
Обратите внимание, что вы не можете победить Arduino. Каждая игра либо заканчивается вничью, либо вы проигрываете, если допустили ошибку. Это потому, что алгоритм всегда выбирает лучший ход. Как вы, возможно, знаете, игра в крестики-нолики всегда заканчивается вничью, если оба игрока не ошибаются. В демо-режиме каждая игра заканчивается ничьей, потому что, как мы все знаем, компьютеры никогда не ошибаются;-)
Шаг 2: минимаксный алгоритм

Алгоритм состоит из двух компонентов: функции оценки и стратегии поиска. Функция оценки - это функция, которая присваивает числовое значение позициям платы. Если позиция является конечной (т. Е. Позиция, в которой либо синий игрок, либо красный игрок выиграли, или где ни один игрок не выиграл), функция оценки очень проста: скажем, Arduino играет синим, а игрок-человек играет красным.. Если позиция является выигрышной для синего, функция присваивает этой позиции значение 10; если это выигрышная позиция для красного, функция присваивает этой позиции значение -10; и если позиция ничья, функция присваивает значение 0.
Когда приходит очередь Arduino, он хочет выбрать ход, который максимизирует значение функции оценки, потому что максимальное значение означает, что он предпочтет победу ничьей (10 больше 0) и предпочтет ничью проигрышу (0 больше -10). Аналогичным образом оппонент хочет играть так, чтобы минимизировать значение оценочной функции.
Для неокончательной позиции алгоритм вычисляет значение функции оценки с помощью стратегии рекурсивного поиска. Начиная с текущей позиции, он поочередно имитирует все ходы, которые могут сделать синий игрок и красный игрок. Это можно представить в виде дерева, как на диаграмме. Когда он достигает конечной позиции, он начинает отступать, перенося значение функции оценки с нижнего уровня рекурсии на более высокий уровень рекурсии. Он присваивает максимальное (если на соответствующем шаге рекурсии ход синего игрока) или минимум (если на соответствующем шаге рекурсии ход красного игрока) значений оценочной функции от нижнего уровня рекурсии до положения на более высокий уровень рекурсии. Наконец, когда алгоритм завершил отступление и снова достиг текущей позиции, он принимает тот ход (или один из ходов), который имеет максимальное значение функции оценки.
Это может показаться немного абстрактным, но на самом деле это не так уж и сложно. Обратите внимание на положение, показанное вверху диаграммы. На первом шаге рекурсии синий может сделать три различных хода. Синий пытается максимизировать значение оценочной функции. Для каждого хода, который может сделать синий, есть два хода, которые может сделать красный. Красный пытается минимизировать значение оценочной функции. Рассмотрим ход, в котором играют синие в правом верхнем углу. Если красное играет в центре поля, красное побеждает (-10). Если, с другой стороны, красный цвет играет в центральном нижнем поле, синий выиграет следующим ходом (10). Таким образом, если синий цвет играет в верхнем правом углу, красный будет играть в центральном поле, поскольку это минимизирует значение функции оценки. Аналогично, если синий цвет играет в центральном нижнем поле, красный снова будет играть в центральном поле, потому что это минимизирует функцию оценки. Если, с другой стороны, синий играет в центре поля, не имеет значения, какой ход сделает красный, синий всегда побеждает (10). Так как синий хочет максимизировать функцию оценки, он будет играть в центральном поле, так как это положение приводит к большему значению функции оценки (10), чем два других хода (-10).
Шаг 3. Устранение неполадок и дальнейшие действия
Если вы нажмете кнопку, и загорится другой светодиод, отличный от того, который соответствует кнопке, возможно, вы перепутали провода на контактах A0-A2 или 4-6, или вы подключили светодиоды в неправильном порядке.
Также обратите внимание, что алгоритм не всегда выбирает ход, который позволит Arduino выиграть как можно быстрее. Фактически, я потратил некоторое время на отладку алгоритма, потому что Arduino не выбрал ход, который был бы выигрышным. Мне потребовалось некоторое время, пока я не понял, что вместо этого он выбрал ход, который гарантировал, что он выиграет один ход позже. Если вы хотите, вы можете попробовать изменить алгоритм так, чтобы он всегда предпочитал выигрышный ход более позднему.
Возможным расширением этого проекта было бы использование алгоритма для создания ИИ для Tic Tac Toe 4x4 или даже 5x5. Однако обратите внимание, что количество позиций, которые необходимо изучить алгоритму, растет очень быстро. Вам нужно будет найти способы сделать функцию оценки более интеллектуальной, присвоив значения позициям, которые не являются окончательными, на основе вероятности того, что позиция хорошая или плохая для данного игрока. Вы также можете попытаться сделать поиск более интеллектуальным, преждевременно остановив рекурсию, если ход окажется менее достойным дальнейшего изучения, чем альтернативные ходы.
Arduino, вероятно, не лучшая платформа для таких расширений из-за ограниченного объема памяти. Рекурсия позволяет стеку увеличиваться во время выполнения программы, и если размер стека слишком велик, это может привести к повреждению памяти программы, что приведет к сбоям или нестабильному поведению. Я выбрал Arduino для этого проекта в основном потому, что хотел увидеть, можно ли это сделать, и в образовательных целях, а не потому, что это лучший выбор для такого рода проблем.
Рекомендуемые:
Самобалансирующийся робот - алгоритм ПИД-регулирования: 3 шага

Самобалансирующийся робот - алгоритм ПИД-регулирования: этот проект был задуман, потому что мне было интересно узнать больше об алгоритмах управления и о том, как эффективно реализовать функциональные контуры ПИД-регулирования. Проект все еще находится в стадии разработки, так как модуль Bluetooth еще не добавлен, что позволит
Распознавание лиц на Raspberry Pi 4B за 3 шага: 3 шага

Обнаружение лиц на Raspberry Pi 4B за 3 шага: в этом руководстве мы собираемся выполнить обнаружение лиц на Raspberry Pi 4 с помощью Shunya O / S, используя библиотеку Shunyaface. Shunyaface - это библиотека распознавания / обнаружения лиц. Проект направлен на достижение максимальной скорости обнаружения и распознавания с помощью
Как установить плагины в WordPress за 3 шага: 3 шага
Как установить плагины в WordPress за 3 шага: в этом уроке я покажу вам основные шаги по установке плагина wordpress на ваш сайт. В основном вы можете установить плагины двумя разными способами. Первый способ - через ftp или через cpanel. Но я не буду перечислять это, потому что он действительно комп
Кордический алгоритм с использованием VHDL: 4 шага
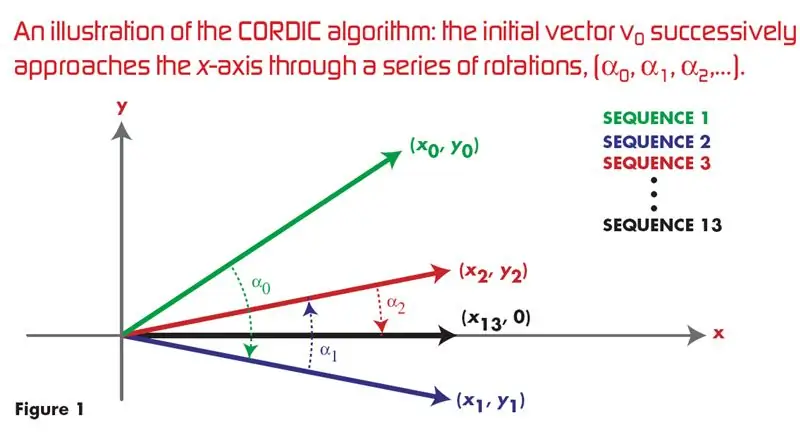
Cordic Algorithm с использованием VHDL: ## Это наиболее посещаемая и популярная ссылка в Google для VHDL-реализации CORDIC ALGORITHM для генерации синусоидальной и косинусной волны ## В настоящее время существует много эффективных аппаратных алгоритмов, но они малоизвестны из-за доминирование softwar
Настольная игра Искусственный интеллект: алгоритм минимакса: 8 шагов
Настольная игра Искусственный интеллект: алгоритм Minimax: Вы когда-нибудь задумывались, как сделаны компьютеры, с которыми вы играете в шахматы или шашки? Не ищите ничего, кроме этого руководства, поскольку оно покажет вам, как создать простой, но эффективный искусственный интеллект (ИИ) с использованием алгоритма Minimax! Используя th
