
Оглавление:
- Шаг 1. Инструменты и материалы
- Шаг 2. Проведение эксперимента
- Шаг 3. Проведение эксперимента
- Шаг 4: Эксперимент: частота дискретизации
- Шаг 5. Эксперимент: отображение шума
- Шаг 6. Эксперимент: уменьшите шум с помощью скользящей средней
- Шаг 7. Эксперимент: скользящее среднее и частота дискретизации
- Шаг 8: Эксперимент: ведение журнала с триггером
- Шаг 9: Эксперимент: регистрация с триггером - громкий шум
- Шаг 10: проводите собственные эксперименты
- Шаг 11: Использование методов в вашем программном обеспечении для ведения журнала
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 11:49.
- Последнее изменение 2025-01-23 15:04.

Есть много инструкций по регистрации данных, поэтому, когда я хотел создать собственный проект регистрации, я просмотрел кучу. Некоторые из них были хорошими, некоторые - не очень, поэтому я решил взять несколько лучших идей и создать свое собственное приложение. В результате получился проект более продвинутый и более сложный, чем я ожидал вначале. Частью этого стала серия экспериментов по обработке сенсорных данных. Это руководство позволяет вам опробовать те же или похожие эксперименты.
(Вы можете просмотреть весь код и загрузить его по адресу: Код на GitHub. Вы можете перейти к просмотру, возможно, в другом окне, всего за 2 клика)
Обычно регистрация данных включает в себя следующее:
- Сбор данных: считывание некоторых данных с датчика. Часто это просто чтение аналого-цифрового преобразователя (АЦП) на таком устройстве, как Arduino.
- Обработка данных: при чтении значения АЦП выходной сигнал преобразователя обычно необходимо масштабировать до правильных единиц. Также может потребоваться некоторая регулировка для калибровки значений для исправления ошибок датчика.
- Фильтрация: данные обычно содержат некоторый шум, его можно отфильтровать, чтобы вы искали сигнал в своих данных, а не шум.
- Хранение данных: данные сохраняются, возможно, в текстовый файл, возможно, в облако. Данные должны сохраняться даже при отключении питания. Слишком много данных легко сохранить, у нас есть небольшая хитрость, чтобы уменьшить пространство для хранения данных.
- Отображение данных: методы просмотра ваших данных, на самом деле не регистрация данных, но если вы не выполняете какое-то отображение данных, зачем их собирать?
- Удаленный доступ: не обязательно, но неплохо иметь.
Большинство инструкций включают некоторые из вышеперечисленных, но не все, или выполняют их очень просто. В этом руководстве будут рассмотрены 2 часто пропускаемые проблемы с журналированием и в качестве бонуса вы получите возможность графического представления данных без использования облачной службы. Вы можете использовать все это целиком или извлекать кусочки и кусочки и переделывать их в собственный проект.
Шаг 1. Инструменты и материалы

Этот пример полностью написан на Python, поэтому он будет работать и компоненты могут использоваться практически на любой ОС, включая Mac, ПК, Linux и Raspberry Pi.
Итак, чтобы использовать эту инструкцию, все, что вам нужно, - это работающая среда Python 3.6 и загрузка прикрепленного кода. После запуска кода, который я настроил, вы можете изменить его для собственных экспериментов. Как обычно с Python, вам может потребоваться добавить несколько пакетов / модулей, чтобы все работало. Моя среда Spyder поставляется с почти всеми необходимыми частями (см.: Графические представления с инструкциями по очистке экрана Python). Когда вы впервые запускаете слежение за любыми сообщениями об ошибках, они сообщают вам о любых недостающих частях в вашей среде.
Следующие два шага расскажут вам, как построить и провести собственный эксперимент, но, вероятно, лучше подождать, пока вы запустите включенные эксперименты, прежде чем пробовать свои собственные.
Чтобы понять код, вам потребуется некоторый опыт работы с объектно-ориентированным Python, объясняя, что это выходит за рамки данной инструкции, но Google должен предоставить вам любую помощь, которая может вам понадобиться.
Обратите внимание на код: (Код на GitHub Вы можете перейти к просмотру, возможно, в другом окне, всего за 2 клика) теперь находится в Python 3.6, поэтому лучше всего иметь 3.6. Более старая версия кода находится здесь по ссылкам ниже.
Шаг 2. Проведение эксперимента
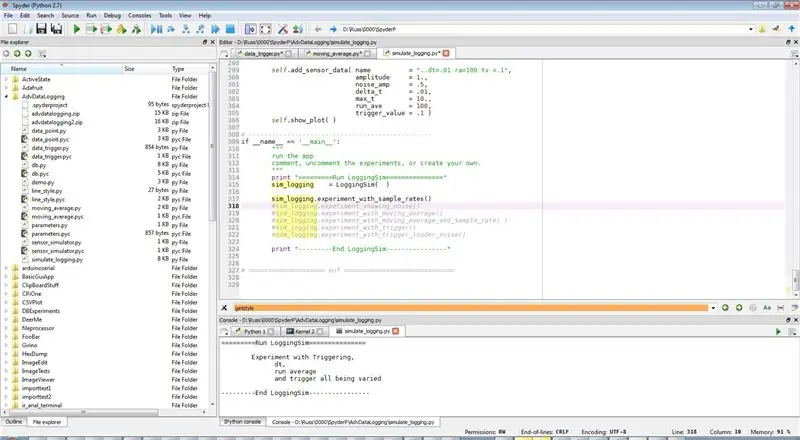
Построение эксперимента состоит из трех программных шагов (и линий). Каждый эксперимент - это функция в объекте LoggingSim в файле simulate_logging.py. Давайте посмотрим на эксперимент 1 (только первый график), который мы запустим на следующем шаге:
def Experiment_with_sample_rates (самостоятельно):
print "" "Эксперимент с частотой дискретизации Просмотр различных частот дискретизации путем изменения дельты T" "" self.start_plot (plot_title = "Sample Rates - Part 1/3: Delta T = 1.0") self.add_sensor_data (name = "dt = 1. ", амплитуда = 1., noise_amp =.0, delta_t = 1., max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot ()
Каждый эксперимент написан как отдельная функция, поэтому у нас есть строка, определяющая функцию (def эксперимент…..)
Следующая строка без комментариев (start_plot (….) Создает объект для эксперимента и дает ему имя.
Следующая строка, не содержащая комментариев, (add_sensor_data (…) разделена на несколько строк. Она имитирует датчик, измеряющий сигнал с потенциально шумом и некоторой обработкой. Аргументы функции следующие:
- имя: имя, нанесенное на окончательный график, чтобы идентифицировать данные
- амплитуда: насколько велик сигнал, в этом руководстве мы всегда будем использовать амплитуду, равную единице.
- noise_amp: насколько велик шум, 0. это не шум, мы начнем с этого.
- delta_t: время между измерениями, контролирует частоту дискретизации.
- max_t: максимальное время сбора данных, в этой инструкции мы всегда будем использовать 10.
- run_ave: обработка с использованием скользящего среднего, 0 означает отсутствие обработки.
- trigger_value: обработка с использованием триггера, 0 означает отсутствие обработки
последняя строка без комментариев (self.show_plot ……) отображает график.
Чтобы немного усложнить задачу, вы можете иметь несколько линий на графике или несколько графиков в эксперименте, это должно быть ясно из следующих экспериментов.
Шаг 3. Проведение эксперимента
Это код для проведения эксперимента. Как и в Python, он помещается в конец файла.
sim_logging = LoggingSim ()
sim_logging.experiment_with_sample_rates ()
Это всего 2 строчки:
- Создайте симулятор ведения журнала (LoggingSim ())
- Запустите его (sim_logging.experiment_with_sample_rates ())
В загруженном коде у меня есть еще несколько строк и комментариев, в этом должно быть легко разобраться.
Шаг 4: Эксперимент: частота дискретизации
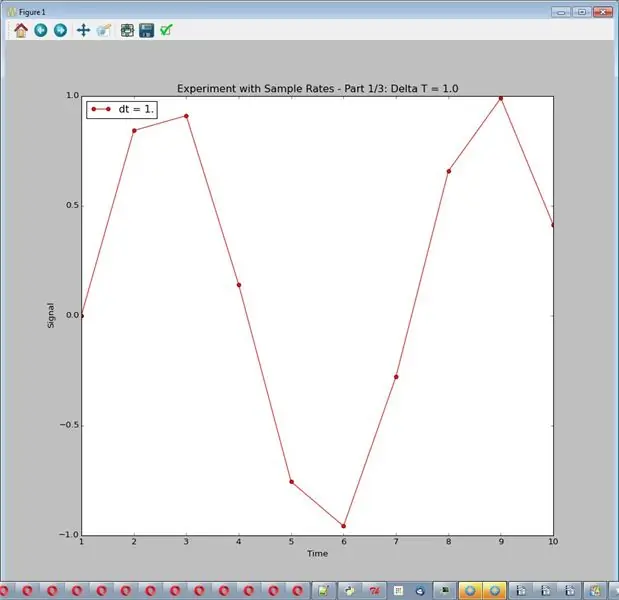
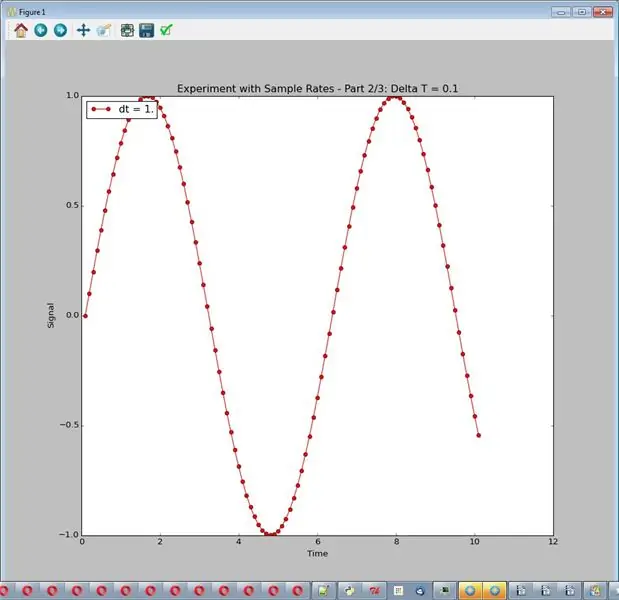
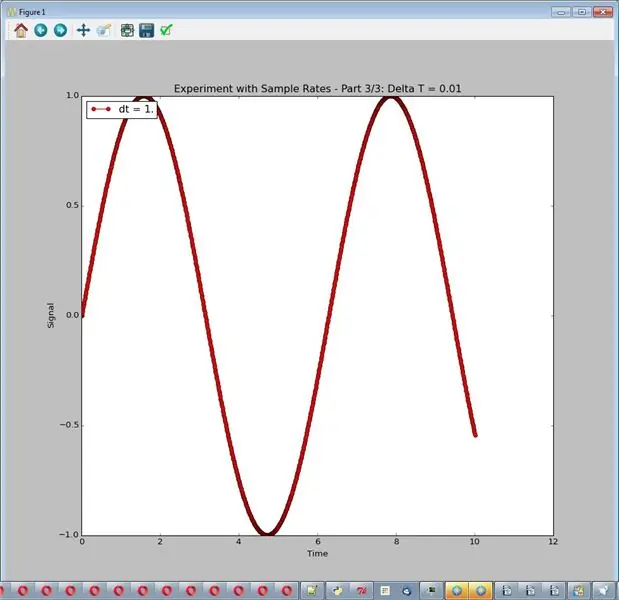
Симулятор, как здесь настроено, всегда выдает красивую гладкую синусоидальную волну амплитуды 1. В этом эксперименте мы будем изменять частоту дискретизации, регулируемую delta_t, разницей во времени между выборками. У нас не будет шума или другой обработки. В коде используются 3 частоты дискретизации (delta_t = 1,0, 0,1 и 0,01). Поскольку графики располагаются один над другим, эксперимент настроен на создание 3 разных графиков. Полученные графики являются изображениями для этого шага.
def Experiment_with_sample_rates (самостоятельно):
print "" "Эксперимент с частотой выборки Просмотр различных частот выборки путем изменения дельты T" "" self.start_plot (plot_title = "Экспериментальные частоты выборки 1/3: Delta T = 1.0") self.add_sensor_data (name = "dt = 1. ", амплитуда = 1., noise_amp =.0, delta_t = 1., max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot () # ------------- ----------------------------------- self.start_plot (plot_title = "Экспериментальная частота выборки 2/3: Дельта T = 0,1 ") self.add_sensor_data (name =" dt = 1. ", амплитуда = 1., noise_amp =.0, delta_t = 0.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot () # ------------------------------------------------ себя.start_plot (plot_title = "Частота выборки эксперимента 3/3: Дельта T = 0,01") self.add_sensor_data (name = "dt = 1.", амплитуда = 1., noise_amp =.0, delta_t = 0,01, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot ()
Для его запуска используйте строку: sim_logging.experiment_with_sample_rates ()
Возможные выводы:
- Слишком низкая частота дискретизации - это действительно плохо.
- Часто лучше высокие ставки.
(Код Python 3.6 на GitHub, ссылка ниже в инструкциях, 2.7)
Шаг 5. Эксперимент: отображение шума
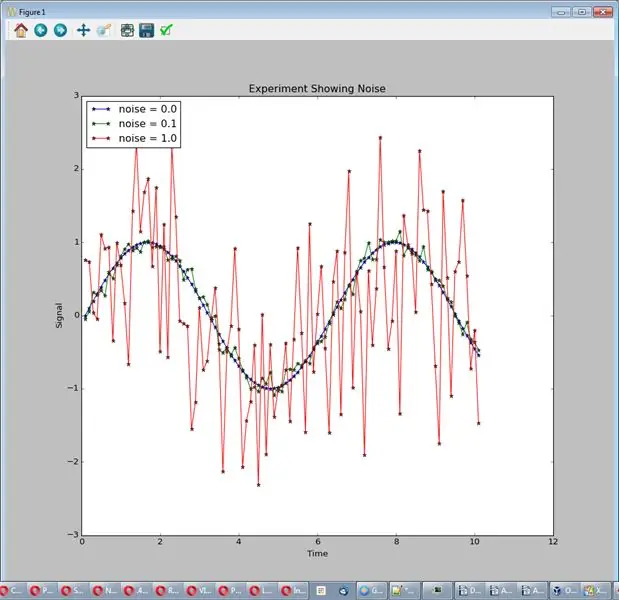
В этом эксперименте мы сохраняем тот же сигнал, используем среднюю частоту дискретизации и разные уровни шума (noise_amp =.0,.1, 1.0.) Запустите его с помощью: sim_logging.experiment_showing_noise (). Результатом является один график с 3 линиями.
Возможный вывод:
Из-за шума трудно увидеть сигнал, по возможности уменьшите его
Код:
# ------------------------------------------------
def Experiment_showing_noise (self): print "" "Эксперимент с отображением шума. Глядя на различные уровни шума путем изменения амплитуды шума." "" self.start_plot (plot_title = "Experiment Show Noise") self.add_sensor_data (name = "noise = 0.0 ", амплитуда = 1., noise_amp =.0, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data (name =" noise = 0.1 ", амплитуда = 1., noise_amp =. 1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data (name = "noise = 1.0", амплитуда = 1., noise_amp = 1., delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot ()
Шаг 6. Эксперимент: уменьшите шум с помощью скользящей средней
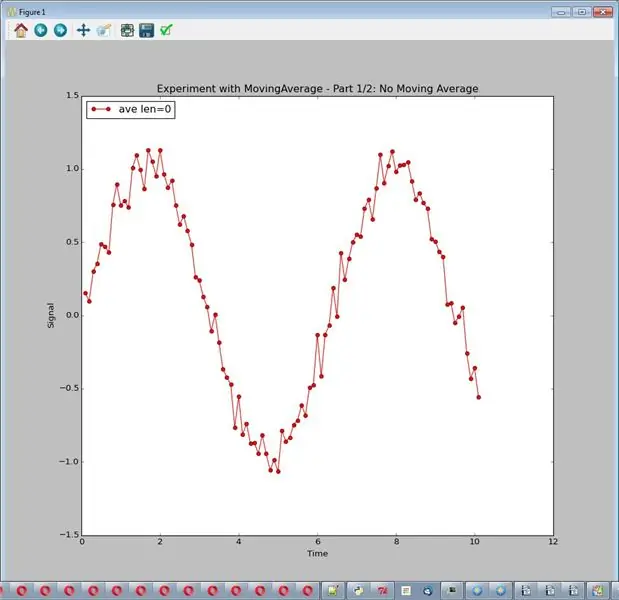
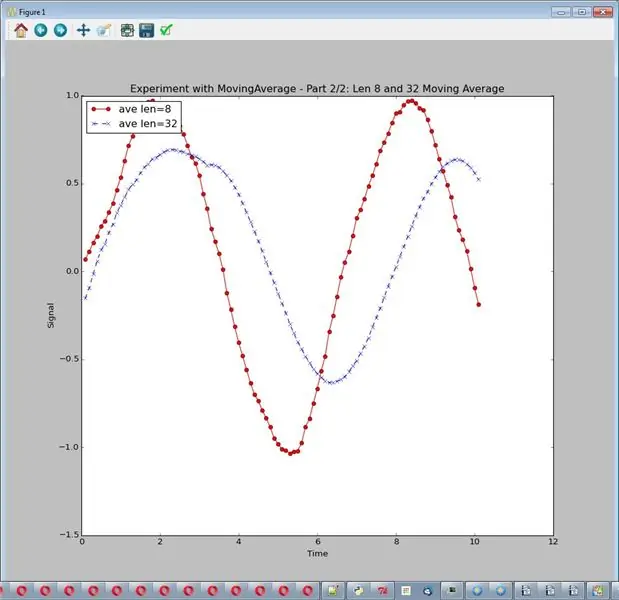
Скользящее среднее (например, с длиной 8) берет последние 8 измерений и усредняет их. Если шум случайный, мы надеемся, что его среднее значение будет около 0. Запустите эксперимент с помощью: sim_logging.experiment_showing_noise (). Выведите один график.
Возможные выводы:
- Скользящее среднее действительно устраняет большую часть шума
- Чем длиннее скользящее среднее, тем больше шумоподавление.
- Более длинная скользящая средняя может уменьшить и исказить сигнал
Код:
# ------------------------------------------------
def Experiment_with_moving_average (self): print "" "Поэкспериментируйте с MovingAverage Глядя на разные MovingAverage, изменяя длину. Все имеют одинаковый шум." "" # ------------------ ------------------------------ self.start_plot (plot_title = "MovingAverage-Part 1/2: No Moving Average") self.add_sensor_data (name = "ave len = 0", амплитуда = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot () self.start_plot (plot_title = "MovingAverage-Part 2/2: Len 8 and 32") self.add_sensor_data (name = "ave len = 8", амплитуда = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 8, trigger_value = 0) self.add_sensor_data (name = "ave len = 32", амплитуда = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 32, trigger_value = 0) self.show_plot ()
Шаг 7. Эксперимент: скользящее среднее и частота дискретизации
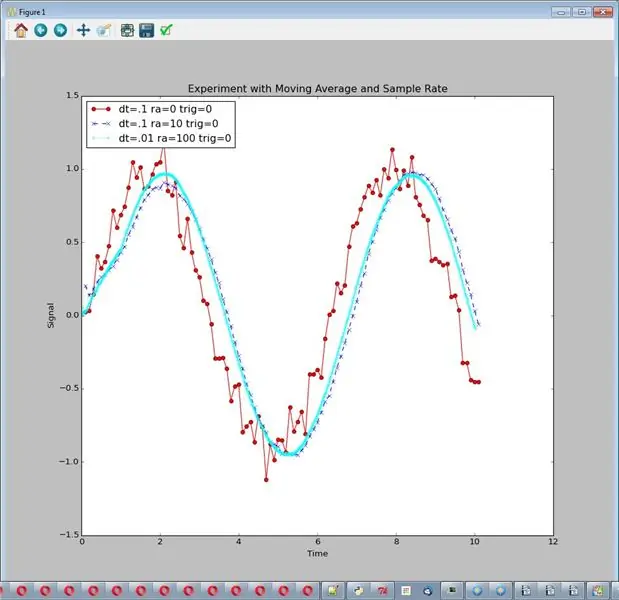
В этом эксперименте мы сравниваем необработанный сигнал с шумом и 2 различных варианта снижения шума.
- Средняя частота дискретизации и среднее бегущее среднее
- Высокая частота дискретизации и большая длина скользящего среднего
Запустите его с помощью: sim_logging …… Вывод - один график. Я думаю, что очевидно, что №2 лучше справляется с уменьшением шума, поэтому мы можем сделать вывод, что:
Высокая частота дискретизации и большая длина скользящего среднего - это хорошо
Но вы должны иметь в виду, что есть цена. №2 требует гораздо большей обработки и приводит к сохранению гораздо большего количества данных. Стоимость может того стоить, а может и не стоить. В следующем эксперименте мы добавим триггер - устройство для уменьшения объема хранимых данных.
Код:
def Experiment_with_moving_average_and_sample_rate (самостоятельно):
print "" "Эксперимент со скользящим средним и частотой дискретизации, dt, среднее значение прогона варьируется" "" # ---------------------------- -------------------- self.start_plot (plot_title = "Moving Average and Sample Rate") self.add_sensor_data (name = "dt =.1 ra = 0 trig = 0 ", амплитуда = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data (name =" dt =.1 ra = 10 trig = 0 ", амплитуда = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data (name = "dt =.01 ra = 100 trig = 0", амплитуда = 1., noise_amp =.1, delta_t =.01, max_t = 10., run_ave = 100, trigger_value = 0) self.show_plot ()
Шаг 8: Эксперимент: ведение журнала с триггером
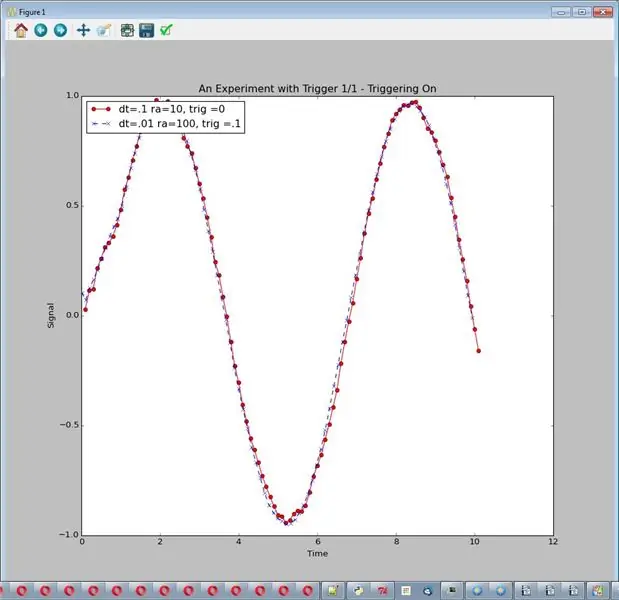
В этом эксперименте мы добавляем триггер. Во-первых, что я имею в виду под триггером? Триггер - это метод, при котором мы собираем данные, но сохраняем их только после значительного изменения какой-либо переменной. В этих экспериментах я ставил триггер на переменную времени (ось x). Используя триггер, я могу взять большой объем данных из быстрой выборки и уменьшить его до более разумного количества данных. Эта особенность полезна при высоких частотах дискретизации и длительном среднем значении.
Я взял строку №2 из последнего эксперимента, которая была "хорошей" и добавила триггер. Запустите его с помощью: sim_logging …… Результат - один график, x строк.
Что происходит? Мы получаем "хороший" график с разумным объемом данных (как №1). Была некоторая стоимость более высокой обработки. В целом, однако, результаты примерно такие же, как №1 - более низкая частота дискретизации с меньшей фильтрацией. Вы можете сделать вывод:
- Длительное среднее значение с запуском может дать хорошее шумоподавление при разумных объемах данных.
- Дополнительная обработка может не дать гораздо лучших результатов и требует затрат.
Код:
# ------------------------------------------------
def Experiment_with_trigger (self): print "" "Экспериментируйте с триггером, dt, средним запуском и триггером, все меняется" "" # ----------------------- ------------------------- self.start_plot (plot_title = "Trigger 1/1 - Triggering On") self.add_sensor_data (name = "dt =.1 ra = 10, trig = 0 ", амплитуда = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data (name =" dt =.01 ra = 100, trig =.1 ", амплитуда = 1., noise_amp =.1, delta_t =.01, max_t = 10., run_ave = 100, trigger_value =.1) self.show_plot ()
=
Шаг 9: Эксперимент: регистрация с триггером - громкий шум
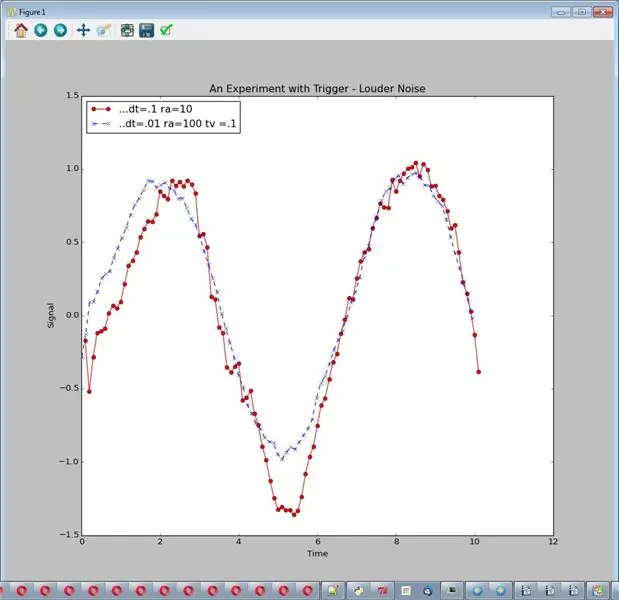
Давайте возьмем тот же эксперимент, что и на последнем шаге, и усилим шум. Запустите его с помощью: sim_logging …… Вывод - один график, 2 строки.
Теперь дополнительная обработка выглядит более целесообразной. Разумным выводом здесь может быть:
Выбор объема и типа обработки для снижения шума зависит от вашего сигнала и шума
Код:
def эксперимент_with_trigger_louder_noise (сам):
print "" "Громче, чем в предыдущем эксперименте" "" self.start_plot (plot_title = "Эксперимент с триггером - громче шум") self.add_sensor_data (name = "… dt =.1 ra = 10", амплитуда = 1., noise_amp =.5, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data (name = "..dt =.01 ra = 100 tv =.1", амплитуда = 1., noise_amp =.5, delta_t =.01, max_t = 10., run_ave = 100, trigger_value =.1) self.show_plot ()
Шаг 10: проводите собственные эксперименты

На этом этапе я надеюсь, что вы видите, что методы, описанные в этом руководстве, могут быть полезны при регистрации данных, но их также нужно использовать с некоторой осторожностью. Эксперименты с ними могут помочь в этом процессе.
Несколько замечаний об экспериментах и вещах, на которые вы могли бы обратить внимание:
- Синусоидальные волны - не единственный интересный тип сигнала, попробуйте другие, другие волны или пандусы или…..
- Я использовал нормальное распределение шума, существует очень много видов шума; ты должен учитывать других
- Средние значения - простой, но не единственный метод определения шума.
Примечание: запись изображений из Википедии.
Шаг 11: Использование методов в вашем программном обеспечении для ведения журнала
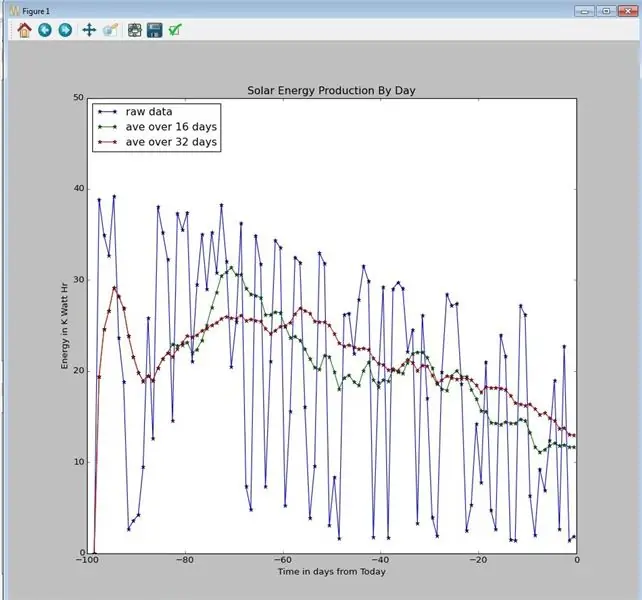
Мой код объектно-ориентирован, и обработку среднего и триггера можно просто скопировать в среду Python и затем использовать. Объектами являются:
- DataTrigger в data_trigger.py
- MovingAverage в moving_average.py
Мой основной объект LoggingSim в simulate_logging.py должен дать вам хороший пример того, как его использовать. Если вы используете другой язык, вы можете прочитать мой код и реализовать его на своем языке.
Этот код может улучшить регистрацию данных в вашем проекте, попробуйте.
График выше взят из Graph Your Solar Power от russ_hensel, в котором используется тот же объект скользящего среднего.
Рекомендуемые:
Как сделать регистратор данных влажности и температуры в реальном времени с Arduino UNO и SD-картой - Моделирование регистратора данных DHT11 в Proteus: 5 шагов
Как сделать регистратор данных влажности и температуры в реальном времени с Arduino UNO и SD-картой | Моделирование регистратора данных DHT11 в Proteus: Введение: привет, это Liono Maker, вот ссылка на YouTube. Мы делаем творческий проект с Arduino и работаем над встраиваемыми системами. Регистратор данных: Регистратор данных (также регистратор данных или регистратор данных) - это электронное устройство, которое записывает данные с течением времени
Построение графика данных датчика температуры в реальном времени (TMP006) с использованием MSP432 LaunchPad и Python: 9 шагов

Построение графика данных датчика температуры в реальном времени (TMP006) с использованием MSP432 LaunchPad и Python: TMP006 - это датчик температуры, который измеряет температуру объекта без необходимости соприкасаться с ним. В этом руководстве мы построим график данных температуры в реальном времени из BoosterPack (TI BOOSTXL-EDUMKII) с использованием Python
Регистратор данных - компьютерный модуль регистрации: 5 шагов
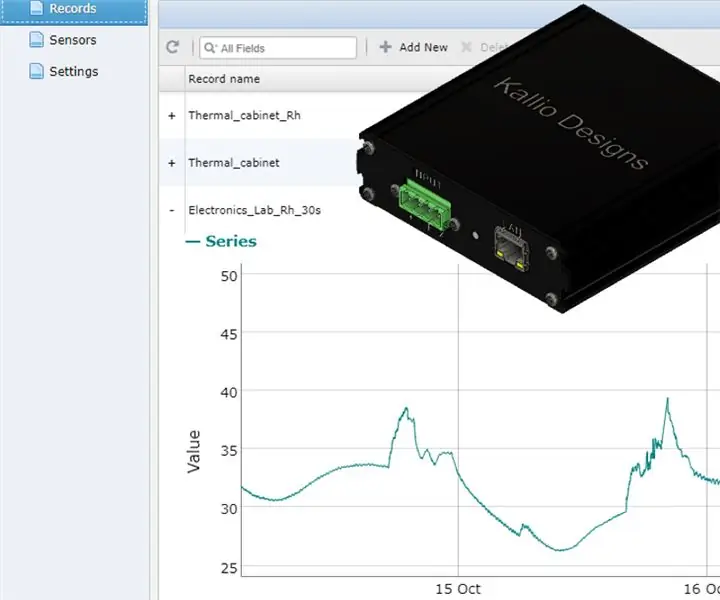
Регистратор данных - компьютерный модуль регистрации: регистратор данных Ethernet для сбора данных на основе HTTP с мостов датчиков, которые преобразуют датчик с интерфейсом I2C в датчик Ethernet
Система посещаемости путем отправки данных RFID на сервер MySQL с использованием Python с Arduino: 6 шагов
Система посещаемости путем отправки данных RFID на сервер MySQL с использованием Python с Arduino: в этом проекте я подключил RFID-RC522 к arduino, а затем отправляю данные RFID в базу данных phpmyadmin. В отличие от наших предыдущих проектов, в этом случае мы не используем какой-либо сетевой экран, здесь мы просто читаем последовательные данные, поступающие из ar
Настройка Raspberry Pi с нуля для регистрации данных с Arduino: 5 шагов

Настройка Raspberry Pi с нуля для регистрации данных с Arduino: это руководство предназначено для тех, у кого нет опыта установки нового оборудования или программного обеспечения, не говоря уже о Python или Linux. Допустим, вы заказали Raspberry Pi (RPi) с SD карта (минимум 8ГБ, я использовал 16ГБ, тип I) и блок питания (5В, минимум 2
