
Оглавление:
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 11:51.
- Последнее изменение 2025-01-23 15:05.
Подписаться Еще от автора:


В классе мы часто используем секундомер, чтобы провести эксперимент с маятником или простой эксперимент с гармоническим движением. Вот вызов: можем ли мы создать реальный график его движения и посмотреть, каковы мгновенные угловое положение и скорость, это намного больше информации и удовольствия.
Первый вопрос: нам нужно решить, что тело маятника представляет собой невесомую веревку или жесткий однородный стержень. Шнур кажется более простым. Из практики создания такой системы у меня есть следующие соображения компромисса: самый простой способ повесить маятниковую систему - это повесить ее на верхний край двери. Это дает вам длину маятника ~ 2 м без каких-либо строительных строительных работ. Но для этого нужно, чтобы качели не касались поверхности двери, что просто испортило весь эксперимент. Таким образом, плоскость поворота должна быть точно параллельна поверхности вашей стены / двери. Невесомый шнур обычно бывает тонким, он легко вращается и затрудняет измерение угла поворота. Мы хотим использовать одно измерение для представления состояния свинга. Тонкий шнур, такой как леска, может быть эластичным и растягивающимся, что влияет на одну из наших самых важных постоянных, измеряемых нами и используемых в уравнении, - длину маятника. На некоторых также может повлиять температура. Вес, висящий на конце шнура, должен быть достаточно тяжелым, чтобы вес шнура был незначительным. Прокомментируйте, если вы согласны или не согласны с ними, или если у вас есть другие дизайнерские идеи компромисса. Чтобы изучить эту проблему, нам нужно устройство, которое настолько легкое, что его вес можно не учитывать, и мы по-прежнему относимся к маятниковой системе как к жесткому однородному стержню. Я использую носимый электронный контроллер COTS, который передает нам информацию о гироскопе, акселерометре и угле через соединение Bluetooth. Эти измерения будут сохранены в файле данных приложения для мобильного телефона. После этого мы проанализируем данные для нашего простого эксперимента с гармоническим движением. Численный анализ фокусируется на следующих темах: 1) Прогнозирование периода колебаний маятника 2) Программный сбор данных эксперимента по простому гармоническому движению маятника 3) Использование kmean для группировки данных и удаления выбросов в процессе анализа 4) Использование краткосрочного БПФ для оценки частота колебаний маятника
Запасы
Измерительный прибор Bluetooth
Приложение для телефона Android: перейдите в магазин Google Play, найдите M2ROBOTS и установите приложение управления. Если получить доступ к Google PlayStore затруднительно, посетите мою личную домашнюю страницу, чтобы узнать об альтернативном методе загрузки приложения
деревянный стержень
несколько деталей, напечатанных на 3D-принтере
пильные диски или аналогичный металлический материал
Шаг 1. Что такое маятник? Как это смоделировать?
Есть много статей и книг, знакомящих с выводом уравнения маятника, включая вашу учебную книгу по физике. Такой контент лучше не повторять здесь снова. Здесь приводится только окончательный вывод по теме «простого гармонического движения». Чтобы узнать период маятника, все, что нам нужно знать, - это длина маятника, обозначенная буквой «l», в метрах.
Если мы достаточно уверены, что груз почти полностью расположен на конце невесомого шнура, висящего на оси, и маятник качается под небольшими углами θ, скажем, менее 15 °, период T1 такого маятника определяется выражением:
T1 = 2 * пи * (л / г) ^ 0,5
g = ускорение свободного падения, примерно 9,8 м / с ^ 2
Если невесомый шнур заменить жестким однородным стержнем, опять же длины l, период его простого гармонического движения T2 будет равен T1 = 2 * pi * (2l / 3g) ^ 0,5.
Фактически, он имеет тот же период, что и у невесомого шнурового маятника, составляющий две трети длины жесткого однородного стержня.
Это предыстория, и мы можем приступить к подготовке эксперимента.
Шаг 2: Подготовьте детали для сборки оборудования



Чтобы построить маятниковую структуру, мы печатаем некоторые детали на 3D-принтере и перерабатываем то, что у нас уже есть. Общая структура маятника показана на рисунке 1. Это смесь деталей, напечатанных на 3D-принтере, некоторых деталей ручной работы и длинного деревянного стержня от Lowe‘s.
Деталь, напечатанная на 3D-принтере на рис. 2, висит на верхнем крае двери, потому что наша дверь - это плоская поверхность, на которой мы можем что-то повесить. Ссылка для скачивания файла STL:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Зеленая часть на рис. 3 соединяет деревянный стержень с лезвием, а лезвие находится поверх двух частей рельса, установленных на ранее напечатанной на 3D-принтере дверной вешалке. Ссылка для загрузки файла STL:
Две части рельса изготавливаются путем сломания старого пильного полотна пополам, см. Рис. 4. В части на рис. 2 для них подготовлен паз нужного размера. В идеале мы можем сделать V-образную выемку на этих двух пильных полотнах с помощью напильника. Металл с достаточно острой кромкой, такой как лезвие бритвы с одной кромкой, или любая металлическая деталь, сделанная вручную, может находиться внутри V-образных выемок. Причина, по которой нам нужна меньшая площадь контакта, состоит в том, чтобы уменьшить кинетическую энергию, потерянную при качании.
Последняя деталь на рисунке 5, напечатанная на 3D-принтере, представляет собой небольшой лоток для размещения электронного измерительного прибора.
Ссылка для скачивания:
Измерительное устройство Bluetooth генерирует оценку угла, гироскопическое измерение и измерение акселерометра. Все эти данные доступны нам через беспроводную связь Bluetooth.
Мы собираемся провести несколько экспериментов, развернув этот аппарат в разных положениях плеча маятника, и увидим различия.
Шаг 3. Сбор данных эксперимента



Есть два выполнимых метода для сбора экспериментальных данных, прежде чем мы проанализируем полученный набор данных:
1) Используйте приложение для телефона Android, указанное в разделе требований, чтобы записать все измерения, произведенные устройством, в файл данных, хранящийся на SD-карте вашего телефона. Мы можем скопировать файл и обработать информацию.
2) Используйте компьютер с поддержкой Bluetooth, ПК, ноутбук или мини-компьютер RaspberryPi, чтобы установить соединение Bluetooth с устройством и прочитать данные для анализа в реальном времени или в автономном режиме.
У каждого метода есть свои плюсы и минусы, мы попробуем оба и расскажем разницу в этой инструкции.
Для метода (1) с использованием приложения Android, как только мы перейдем в интерфейс управления приложением Android, данные телеметрии, отправленные с измерительного устройства Bluetooth на телефон Android, будут записаны в файл журнала данных с именем m2flightDatayyyymmdd_hhmmss.txt. Его можно найти в папке Download / m2LogFiles вашего телефона Android. Папка «Download» - это уже существующая папка в ОС Android вашего телефона, а «m2LogFiles» - это папка, созданная приложением. Содержимое файла yyyymmdd_hhmmss - это способ кодирования времени начала эксперимента (год, месяц, день, час, минута и секунда) в имени файла.
Каждая строка в файле журнала представляет собой одну запись. Он начинается с метки времени события, строки преамбулы «eam:», за которой следуют 4 триплета данных, а именно:
Показания оси XYZ акселерометра в необработанных значениях считывания аппаратного регистра датчика
Считывание оси XYZ гироскопа в необработанных значениях считывания аппаратного регистра датчика
Показания оси XYZ магнитометра в исходных значениях считывания аппаратного регистра датчика
бортовая оценка Roll / Pitch / Raw в градусах
Файл данных, созданный с помощью компьютерной программы python, будет использовать идентичный формат файла данных, поэтому программу, которую мы используем на этапе анализа данных, не будет беспокоить источник данных, созданный нашей программой python или приложением для Android.
Приступим к кодированию по методу (2).
Для взаимодействия с измерительным устройством Bluetooth предусмотрены две разновидности SDK:
1) Python SDK, который можно установить с помощью «pip3 install m2controller», используемый язык - python3. Примеры кода пользовательского приложения хранятся в https://github.com/xiapeiqing/m2robots/tree/maste … Для этого эксперимента мы будем использовать скрипт python pendulum1.py
2) Java SDK, который не используется в этом руководстве, потому что нам нужна более поздняя визуализация и анализ полученных данных маятника, что может потребовать немного больше усилий для программирования на Java.
Исходный код программы сбора данных python3 содержит много комментариев для деталей функциональности кода. Здесь представлен снимок исходного кода.
#! / usr / bin / env python # - * - кодировка: UTF-8 - * - из m2controller import m2controller из m2controller import m2Const import signal import time import datetime import usrCfg import pendulum2
requestExit = Ложь
################################################################
# мы хотим использовать то же соглашение об именах файлов журнала, чтобы модуль анализа данных, pendulum2.py, мог не зависеть от того, как мы получаем файл данных журнала ################ ############################################ logfilename = " m2flightData% s.txt "% (datetime.datetime.fromtimestamp (time.time ()). strftime ('% Y% m% d_% H% M% S')) dataLogfile = open (имя файла журнала," w ")
def signal_handler (sig, frame):
global requestExit print ('пользователь Ctrl-C для выхода из выполнения программы') requestExit = True signal.signal (signal. SIGINT, signal_handler)
################################################################
# после того, как данные каждого измерения станут доступны с частотой 20 Гц, будет вызвана эта функция «обратного вызова» ############################## ############################### def callbackfunc (телеметрия): strTimeStamp = datetime.datetime.fromtimestamp (time.time ()). strftime ('% H:% M:% S.% f') [: - 3] dataStr = "% s, eam:% d,% d,% d,% d,% d,% d,% d,% d,% d,% 2.1f,% 2.1f,% 2.1f / n "% (strTimeStamp, телеметрия ['m_fAccelHwUnit'] [0], телеметрия ['m_fAccelHwUnit'] [1], телеметрия ['m_fAccelHwUnit'] [2], телеметрия ['m_fGyroHwUnit'] [0], телеметрия ['m_fGyroHwUnit'] [1], телеметрия ['m_fGyroHwUnit'] [2], телеметрия '[' m_fMagHw] 'm_fMagHwUnit'] [1], телеметрия ['m_fMagHwUnit'] [2], телеметрия ['m_fRPYdeg'] [0], телеметрия ['m_fRPYdeg'] [1], телеметрия ['m_fRPYdeg'] [2]) ## #################################################################################################### ############ # выводим строку данных на экран и сохраняем в файл журнала ##################### ################################################################################### print (dataStr) dataLogfile.writelines (dataStr)
################################################################
# инициализировать контроллер, не забудьте установить в поле BleMACaddress MAC-адрес вашего устройства ############################### ############################# # TODO: давайте инициализируем BleMACaddress, если он не установлен пользователем. controller = m2controller. BleCtrller (m2Const.etDebian, callbackfunc, usrCfg. BleMACaddress) controller.connect () while True: ######################### #################################### # ждать данных измерений, созданных и отправленных из измерения маятника аппарат ########################################################################## ############### controller.m_CommsTunnel.waitForNotifications (1.0) if requestExit: ###################### ##########################################################################################################}> ########################################################################### ############## controller.stop () dataLogfile.close () break
################################################################
# сбор данных завершен, теперь давайте проанализируем данные журнала ######################################################################## ######################## pendulum2.parseDataLogFile (имя файла журнала)
Для долгосрочного обновления, пожалуйста, проверьте
Теперь объясним способ его работы. Эта программа на Python написана поверх устанавливаемого пакета pip с именем m2controller. Пакет нижнего уровня предлагает механизм обратного вызова, так что каждое полученное обновление измерений запускает написанную нами функцию обратного вызова и сохраняет данные в локальном файле журнала. Формат содержимого данных файла журнала идентичен формату, создаваемому сопутствующим приложением Android, поэтому файл журнала данных, созданный программой python или сопутствующим приложением andriod, можно заменять.
Пользовательский сигнал ctrl-C, захваченный операционной системой, передается программе и останавливает бесконечный цикл, ожидая нового поступления данных измерения.
К настоящему моменту файл журнала был успешно создан, и эта программа будет вызывать программу анализа для изучения результатов нашего эксперимента.
Вот два эксперимента, и сравнение показывает очень заметную разницу при подключении 7-граммового устройства в разных местах.
На рисунке 2 мы используем шкалу для определения фактического веса этого измерительного устройства Bluetooth.
На рис.3 изображена маятниковая установка, в которой 7-граммовое устройство прикреплено к нижнему концу маятника. Конфигурация установки на рис. 4 имеет массу в 7 грамм, расположенную намного ближе к поворотной оси.
Фиг.5 представляет собой крупный план конструкции маятника.
Шаг 4: Анализ данных



Измерительный прибор Bluetooth весит ~ 7 граммов, что намного меньше, чем деревянная палка длиной ~ 1,6 метра. Используйте предположение о «жестком однородном стержне», и у нас есть это уравнение периода маятника, T1 = 2 * pi * (2l / 3g) ^ 0,5.
Чтобы получить гравитационную постоянную, мы можем использовать 9,8 м / с ^ 2. Но более точную постоянную силы тяжести для любой заданной геолокации можно получить с помощью этого веб-сервиса:
www.wolframalpha.com/widgets/view.jsp?id=e…
Для Сан-Франциско это 9,81278 м / с ^ 2.
Длина маятника составляет 64,5 дюйма.
2 * pi * sqrt (2 * 64,5 * 0,0254 / (3 * 9,81278)) дает ожидаемый период маятника 2,0962 (сек).
Посмотрим, согласуется ли это с нашими экспериментами.
В первом эксперименте маятниковая установка имеет 7-граммовое устройство, прикрепленное к нижнему концу маятника. Мой файл журнала можно скачать в:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Переименуйте его в «PendulumTestData.txt» и поместите в ту же папку программы анализа Python. Здесь представлен снимок исходного кода.
#! / usr / bin / env python # - * - coding: UTF-8 - * - import csv import matplotlib.pyplot as plt plt.style.use ('seaborn-whitegrid') import numpy as np from datetime import datetime, timedelta import seaborn as sns from sklearn.cluster import KMeans from collection import Counter ################################################################ ############################ # эта функция запускает работу по анализу файла данных ############ #################################################################################################### ## def parseDataLogFile (имя файла данных): ################################################################################################## ##################### # извлеките данные из файла журнала данных, разделенных запятыми (CSV), и сохраните содержимое каждого столбца в одну переменную типа float ## #################################################################################################### ############ с open (имя файла данных) как csvfile: readCSV = csv.reader (csvfile, delimiter = ',') timestampS = fAccelHwUnit_x = fAccelHwUnit_y = fAc_z_zwUnit fGyroHwUnit_x = fGyroHwUnit_y = fGyroHwUnit_z = fMagHwUnit_x = fMagHwUnit_y = fMagHwUni t_z = fRPYdeg_r = fRPYdeg_p = fRPYdeg_y = для строки в readCSV: попробуйте: x = datetime.strptime (row [0].split (',') [0], '% H:% M:% S.% f ') timestampS.append (timedelta (часы = x.hour, minutes = x.minute, секунды = x.second, microseconds = x.microsecond).total_seconds ()) fAccelHwUnit_x.append (float (row [1] [4:])) fAccelHwUnit_y.append (float (строка [2])) fAccelHwUnit_z.append (float (строка [3])) fGyroHwUnit_x.append (float (строка [4])) fGyroHwUnit_at_at_at.append (float (строка [4])] (строка [5])) fGyroHwUnit_z.append (float (row [6])) fMagHwUnit_x.append (float (row [7])) fMagHwUnit_y.append (float (row [8])) fMagHwUnit_z.append (float (row [9])) fRPYdeg_r.append (float (row [10])) fRPYdeg_p.append (float (row [11])) fRPYdeg_y.append (float (row [12])) за исключением: передать timestampS = np.asarray (Timestamps) Timestamps = Timestamps - Timestamps [0] = fAccelHwUnit_x np.asarray (fAccelHwUnit_x) fAccelHwUnit_y = np.asarray (fAccelHwUnit_y) fAccelHwUnit_z = np.asarray (fAccelHwUnit_z) fGyroHwUnit_x = np.asarray (fGyroHwUnit_x) fGyroHwUnit_y = np.asarray (fGyroHwUnit_y) fGyroH wUnit_z = np.asarray (fGyroHwUnit_z) fMagHwUnit_x = np.asarray (fMagHwUnit_x) fMagHwUnit_y = np.asarray (fMagHwUnit_y) fMagHwUnit_z = np.asarray (fMagHwUnit_z) fRPYdeg_r = np.asarray (fRPYdeg_r) fRPYdeg_p = np.asarray (fRPYdeg_p) fRPYdeg_p = fRPYdeg_p - np.mean (fRPYdeg_p) fRPYdeg_y = np.asarray (fRPYdeg_y)
################################################################
# нам нужна точная оценка частоты дискретизации для точной оценки периода колебаний ################################### ########################### FsHz = getSamplingIntervalS (timestampS) ############### ################################################ # использовать компонент шага в выходных данных системы отсчета заголовка для маятникового анализа периода ################################### ########################## analysis_timeSequence (timestampS, fRPYdeg_p, FsHz, 'pitch') ########### #################################################################################################### ### # использовать исходные результаты измерений акселерометра для анализа маятникового периода ####################################################### ########################## analysis_timeSequence (timestampS, fAccelHwUnit_x, FsHz, 'ускорение') ########### #################################################################################################### ### # использовать исходные данные измерений гироскопа для анализа периода маятника ###################################################### ########################## analysis_timeSequence (timestampS, fGyroHwUnit_y, FsHz, ' gyro ') print (' готово, поздравляем:-) ') plt.show () ############################## ################################ # # в процессе связи Bluetooth существует редкая вероятность того, что пакет передачи данных может be lost # мы используем K-mean, чтобы изолировать данные измерений с частотой 20 Гц от выбросов, которые вызваны потерянным пакетом # погрузитесь в "сигнал и систему для более подробной информации" ################ ############################################ def getSamplingIntervalS (timestampS): plt.figure () sampleIntervalS = np.diff (timestampS) sns.distplot (sampleIntervalS) plt.ylabel ('histogram') plt.xlabel ('measurement interval (s)') clusterCnt = 5 km = KMeans (n_clusters = clusterCnt) km.fit (sampleIntervalS.reshape (-1, 1)) centroids = km.cluster_centers_ elemCnt = Counter (km.labels_) instanceCnt = for ii in range (clusterCnt): instanceCnt.append (elemCnt [ii]) FsHz = 1 / centroids [instanceCnt.index (max (instanceCnt))] возвращает FsHz
################################################################
# использовать спектрометр, т.е. кратковременное БПФ для получения частотной составляющей, пиковый интервал - наша лучшая оценка колебания маятника ######################### ################################### def analysis_timeSequence (timestampS, timeSeqData, FsHz, strComment): fig, (ax1, ax2) = plt.subplots (nrows = 2) ax1.plot (timestampS, timeSeqData, marker = 'o', markerfacecolor = 'blue', markersize = 2, color = 'skyblue', linewidth = 1) ax1.set_title («маятниковое измерение во временной области -% s»% strComment) ax1.set_xlabel («время выборки (секунда)») ax1.set_ylabel (strComment); NFFT = 2048 # длина оконных сегментов
Pxx, freqs, bin, im = ax2.specgram (timeSeqData, NFFT = NFFT, Fs = FsHz, noverlap = NFFT / 2)
ax2.set_title ("Спектрограмма") ax2.set_xlabel ("образцы") ax2.set_ylabel ("частота (Гц)");
# Метод `specgram` возвращает 4 объекта. Они есть:
# - Pxx: периодограмма # - freqs: вектор частот # - интервалы: центры интервалов времени # - im: экземпляр matplotlib.image. AxesImage, представляющий данные на графике pkresult = np.where (Pxx == np.amax (Pxx)) oscFreqHz = freqs [pkresult [0] [0] print ('Частота колебаний маятника (Гц) =% f, Период (Сек) =% f, источник данных оценки:% s'% (oscFreqHz, 1 / oscFreqHz, strComment)) return 1 / oscFreqHz
################################################################
# если мы запускаем эту программу независимо, т.е. не вызывая ее из pendulum1.py, # мы определяем имя файла данных журнала по умолчанию для анализа #################### ################################################################### if _name_ == "_main_ ": defaultFilename = './PendulumTestData.txt' import os.path if os.path.isfile (defaultFilename): parseDataLogFile (defaultFilename) else: print (" Файл журнала по умолчанию% s не существует "% defaultFilename)
Для долгосрочного обновления, пожалуйста, проверьте
Исходный код содержит подробные комментарии, давайте дадим здесь краткое изложение математической оценки.
1) Сначала мы считываем содержимое файла CSV в компьютер, используя пакет Python под названием «csv». У нас есть периодические замеры.
21: 34: 26.362, eam: 0, -128, 14464, -8, 144, -96, 2112, -1280, 1664, -0,5, -5,5, 40,5
21: 34: 26.373, eam: 128, 0, 14272, -8, 136, 40, 2112, -1280, 1664, -0,5, -6,5, 40,0
21: 34: 26.412, eam: 448, -64, 14208, -8, 136, 24, 2176, -1280, 1664, -0,5, -7,5, 40,5
21: 34: 26.462, eam: 448, -128, 14272, -8, 120, 16, 2176, -1280, 1664, -0,5, -8,0, 40,5
2) Поскольку скорость измерения очень важна и напрямую вносит погрешность в оценку периода маятника, мы хотим их оценить. Наш номинальный интервал измерения составляет 50 мс, то есть 20 Гц. Среднее значение по всем измерениям кажется нормальным, но иногда мы теряем пакет передачи данных, интервал обновления становится 100 мс или 150 мс,…
Если мы построим график появления этих данных, см. Рис. 1, как человек, мы легко можем получить визуальное значение 0,05 секунды. Однако можем ли мы сделать лучше, чем это?
Нам нужно использовать метод классификации, чтобы выбрать только хорошие для вычисления усреднения. У Python есть набор инструментов под названием KMeans, который помогает нам с кластеризацией или, скажем, классификацией. Эти концепции используются во многих областях больших данных и искусственного интеллекта.
3) Рис.2 содержит два изображения. Верхний график представляет собой временную последовательность наших измерений угла поворота в градусах. Ссылаясь на временную метку оси x в секундах, мы можем прочитать приблизительно 22,5 цикла за 50 секунд, что соответствует периоду маятника 2,22 секунды. Есть ли способ автоматизировать этот процесс и получить более точную оценку? Да, мы можем использовать математический инструмент, называемый спектрограммой, который использует небольшой фрагмент данных измерений и сообщает нам его частоту, см. Рисунок ниже. По оси ординат самая темная линия - это частота колебаний маятника. Горизонтальная линия подтверждает, что колебания маятника не менялись на протяжении всего эксперимента. Обратной величиной частоты колебаний является период колебаний маятника.
Итоговый отчет, сделанный программой, представляет собой текстовое резюме:
колебания маятника Freq (Hz) = 0.449224, Period (Sec) = 2.226059, источник данных оценки: шаг
Мы можем обнаружить, что наш предыдущий результат вычисления руки на глаз, 2,22 секунды, довольно согласуется с вычисленным программой значением.
По сравнению с теоретически рассчитанным значением 2,0962 (сек), остающаяся ошибка составляет ~ 5%. Как от них избавиться? Помните предположение о «жестком однородном стержне»? Даже 7-граммовый лишний вес кажется тривиальным, это основная причина оставшейся ошибки.
Теперь переместим устройство ближе к оси. См. Предыдущий шаг для получения фотографии крупным планом. Созданный мной файл журнала можно скачать здесь:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Выполните те же шаги анализа, и мы получим период 2,089867 (сек), см. Рис. 3, который почти идентичен теоретическому предсказанию. Большой!
Поскольку у нас есть не только измерение угла поворота, но и гироскопическое измерение, и измерение акселерометра с той же скоростью. Выполните тот же анализ для двух других измерений, мы получим результаты на рисунках 4 и 5. Оценки всех трех источников измерений совпадают, что делает нас более уверенными в успехе нашего эксперимента.
Вот результат как окончательный результат работы программы python:
колебания маятника Freq (Hz) = 0.478499, Period (Sec) = 2.089867, источник данных оценки: шаг
колебания маятника Freq (Hz) = 0.478499, Period (Sec) = 2.089867, источник данных оценки: ускорение
колебания маятника Freq (Hz) = 0.478499, Period (Sec) = 2.089867, источник оценочных данных: гироскоп
Последняя мысль на этом этапе: как результаты оценки могут быть точно идентичными при использовании разных источников входных данных? Это противоречие. Я оставлю этот вопрос читателям. Вот подсказка: помните, мы используем кратковременное БПФ для оценки частоты колебаний? В цифровой области оценка частоты дается в дискретных элементах разрешения по частоте вместо оценки с плавающим числом.
Шаг 5: Рекомендации для будущей работы
Есть несколько категорий рекомендаций по будущей работе.
На более раннем этапе нам удалось уменьшить ошибку нашего эксперимента с ~ 5% до менее 1%, можем ли мы сделать лучше, чем это? Заметив, что величина колебаний уменьшается экспоненциально, одним из факторов может быть сопротивление воздуха, возникающее при раскачивании маятника. Возможно, потребуется изменить поперечное сечение маятника, чтобы оно имело обтекаемую форму, чтобы уменьшить аэродинамическое сопротивление.
Можем ли мы применить изменяющееся во времени усиление, полученное с помощью методов адаптивной фильтрации, для вывода сигнала с постоянной пиковой амплитудой. А пока соотносим величину затухания с внешними силами.
Трудно найти что-то более простое, чем «простое гармоническое движение». Можем ли мы использовать средства, с помощью которых мы анализируем маятник, для анализа чего-то более сложного, спортивного занятия, последовательности запуска водяной ракеты и т. Д.?
Удачного взлома
Рекомендуемые:
Создание простого робота из вещей, которые вы можете найти в своем доме (версия с колесиком): 5 шагов

Создание простого робота из вещей, которые вы можете найти в своем доме (версия с горячим колесом): это руководство покажет вам, как сделать самоуправляемое колесо, работающее от батареек типа «двойное А». Вам нужно будет использовать только те вещи, которые, скорее всего, найдете в вашем доме. Обратите внимание, что этот робот, вероятно, не пойдет точно по прямой, а
Исследование моделирования: 9 шагов
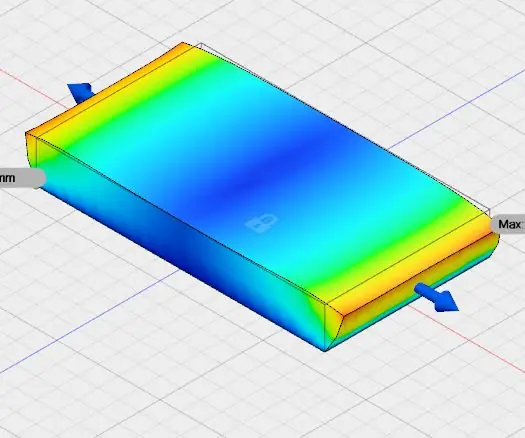
Исследование моделирования: в этом руководстве я использовал fusion 360 от Autodesk. Это руководство предназначено для исследования моделирования. В нем я использовал модель и рабочее пространство моделирования auto desk fusion 360. Я изучил моделирование для продольных сил величиной 10 Н
Исследование пыли Arduino: 8 шагов

Arduino Dust Study: каково было бы жить на Марсе? Воздух пригоден для дыхания? Это безопасно? Сколько там пыли? Как часто бывают бури? Вы когда-нибудь задумывались над ответом на любой из этих вопросов?
Исследование эффекта резонансной структуры с помощью бумажных сот: 6 шагов

Исследование эффекта резонансной структуры с помощью бумажных сот: я подумал, что те, кто любит заниматься альтернативными источниками энергии, могли бы попробовать это. В его основе лежит открытие Виктора Гребеннкова. Эту историю можно найти во многих местах, но я нашел эту на keelynet http://www.keelynet.com/gr
Выходное отверстие с контролем движения - от датчика движения: 6 шагов

Выходное отверстие с контролем движения - от источника света с датчиком движения: Представьте, что вы обманщик, идущий в самый страшный дом в квартале. Пройдя мимо всех гулей, привидений и кладбищ, вы наконец доберетесь до последнего пути. Вы видите перед собой конфету в миске! Но тут вдруг гхо
