3D-реконструкция по одной фотографии: 8 шагов

2024 Автор: John Day | [email protected]. Последнее изменение: 2024-01-30 11:48

Задача 3D-реконструкции обычно связана с бинокулярным зрением. Как вариант, вы можете перемещать одиночную камеру вокруг объекта. Между тем, если форма объекта известна, задача может быть решена по одной фотографии. То есть у вас только одна камера, и она не двигается. Давайте посмотрим, как это сделать пошагово. Мы будем использовать кубик Рубика, потому что он хорошо стандартизирован и имеет богатый набор функций. Его можно рассматривать как очень простой объект и одновременно сложную конструкцию. Таким образом, машинное зрение должно преодолевать существенные препятствия, чтобы выполнить задачу.

Шаг 1. Оцените сложность задачи

На первый взгляд задача простая. Найдите центральный узел, в котором сходятся 3 ребра куба, и нарисуйте эти ребра. По их координатам можно рассчитать расстояние до камеры и углы поворота. Проблема в том, что этих строк не существует. На левом изображении вы видите, что каждый край представлен двумя параллельными линиями. Кроме того, на верхнем правом рисунке видно, что каждый из них разбит на 3 сегмента. Более того, если мы применим вариант популярного преобразования Хафа, которое может обнаруживать отрезки линии, оно выполняет задачу с некоторыми ошибками, которые делают невозможным обнаружение центрального узла. Если концы не доходят друг до друга, нет единой точки. Если обнаружение выходит за край, он будет выглядеть как узел посередине края, как вы видите на двух оставшихся изображениях.

Шаг 2: Найдите правильный подход

Когда слишком много деталей делает детерминированные алгоритмы неработоспособными, пора рассмотреть вероятностный подход. Если рассчитать усредненные параметры изображения, их погрешности существенно уменьшатся и, как это ни парадоксально, метод окажется более надежным. Стандартное преобразование Хафа не выводит линейные сегменты. Только его наклон theta и расстояние rho от начала координат. Они образуют пространство Хафа, часть которого показана выше. Здесь тета соответствует горизонтальной оси. Яркими точками отмечены возможные линии на изображении. Обратите внимание, что несколько таких точек расположены одно над другим. Неудивительно, что на нашем изображении много параллельных линий. У них одинаковая тета и разные ро.

Шаг 3. Рассчитайте тета-гистограмму

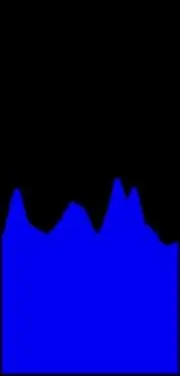
Обнаружим такие кластеры. Для этого мы суммируем показания для всех точек в пространстве Хафа с одинаковой тэтой. Вы видите соответствующую гистограмму на иллюстрации. Несколько замечаний об измерениях. Когда вы работаете с изображениями в пиксельных координатах, ось X движется как обычно, но Y указывает вниз, поэтому начало координат находится в верхнем левом углу, а тета должна измеряться от оси X по часовой стрелке. Имея в виду, что весь разворот теты на изображении составляет 180 градусов, вы можете приблизительно проверить, что 3 основных пика представляют 3 преобладающих наклона на изображении.

Шаг 4: Рассчитайте гистограмму Rho

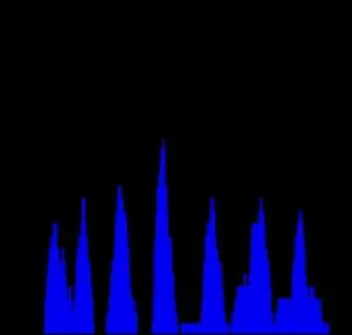
Теперь, когда мы знаем 3 основных группы параллельных линий, давайте разделим линии внутри каждого из них. Мы можем повторить тот же подход. Возьмем столбец из пространства Хафа, который соответствует одному пику на тета-гистограмме. Затем мы рассчитаем еще одну гистограмму, где ось X представляет значение rho, а Y - итоговые показания для этого rho. Очевидно, что сумма будет меньше, поэтому график получится не таким гладким. Тем не менее, пики хорошо видны, и количество их (7) точно соответствует количеству параллельных линий на исходном изображении. К сожалению, не все графики так совершенны, но принцип ясен.

Шаг 5: Найдите центральный узел

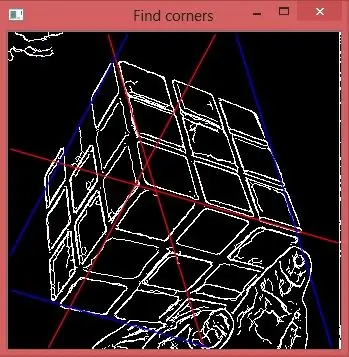
Если мы возьмем центральный пик на гистограмме для каждой тэты, мы получим 3 линии, которые на картинке красные. Их пересечение отмечает нужную точку.

Шаг 6: выберите один из двух вариантов

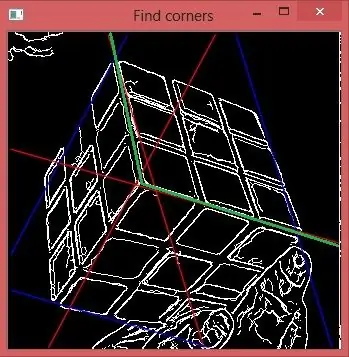
Вы видите, что каждая линия идет от центральной точки в обоих направлениях. Как определить правильную половину? Возьмем theta3. Допустим, мы берем нижнюю часть этой линии. Рассчитаем еще одно пространство Хафа только для части изображения от 2-х зеленых линий до правого верхнего угла изображения. Затем создайте для него тета-гистограмму. Вы видите, что третий пик полностью исчез, значит, мы сделали правильный выбор.

Шаг 7: Определите внешние углы

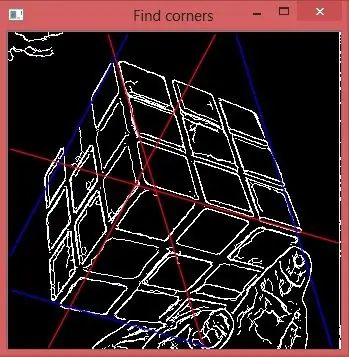
Теперь мы можем использовать первый и последний пик на ро-гистограммах, чтобы нарисовать синие линии, которые срезают красные края и отмечают остальные углы. Задача решена.

Шаг 8: попробуйте на практике

Иллюстрации к этому Учебному пособию были созданы с использованием Perception 1.0. Это бесплатное программное обеспечение, использующее OpenCV - мощную библиотеку для компьютерного зрения. Также он может быть связан с WinNB, который использовался в моем другом Instructable, тем самым обеспечивая возможности машинного зрения для робототехники. Вы можете скачать обе программы с сайта. Для установки просто запустите скачанный exe-файл. Позже вы сможете удалить его стандартным инструментом Windows. На сайте также есть ресурсы по компьютерному зрению и смежным темам. В Perception вы найдете описанный метод трехмерной реконструкции, а также многие другие. Преимущество этой программы в том, что она выводит окончательный результат вместе с промежуточными данными. Вы можете исследовать, как работает компьютерное зрение, не будучи программистом. Что касается ввода, то для каждого метода специально отобраны типовые образцы. Конечно, вы можете использовать и свой собственный. Можно вводить изображения из файла или с камеры компьютера. Не стесняйтесь обращаться ко мне с любыми вопросами или предложениями.